Dalam ilmu matematika, ada banyak sekali jenis bilangan. Salah satunya adalah bilangan berpangkat yang disebut juga sebagai eksponen. Sangat penting untuk mendalami bilangan eksponen karena nantinya bilangan ini akan menjadi suatu ilmu dasar yang sangat berguna dalam hitung-menghitung.
Bilangan eksponen bisa digunakan untuk membantu perhitungan yang melibatkan banyak sekali angka serta untuk menyelesaikan persamaan. Berkat adanya bilangan pangkat, perhitungan dengan banyak angka bisa diselesaikan dengan lebih cepat. Itulah sebabnya bilangan pangkat sangat penting.
Mengenal Bilangan Pangkat atau Eksponen
Sederhananya, bilangan eksponen atau pangkat merupakan perkalian antara suatu bilangan yang nilainya sama. Perkalian dilakukan sesuai dengan jumlah pangkat. Sebagai contoh, jika angka 3 dikalikan dengan angka 3 sebanyak 5 kali, maka akan menjadi 3x3x3x3x3.
Jika diubah menjadi bilangan pangkat maka hasilnya adalah 3 pangkat 5 atau 35. Dari keterangan inilah maka bilangan pangkat bisa dituliskan dengan suatu rumus tertentu, yaitu an=axaxaxax…xa. Dalam bilangan pangkat ada beberapa sifat yang harus dipahami.
Rumus umum diatas hanya berlaku untuk pangkat yang nilainya positif saja. Lalu bagaimana kalau pangkatnya mempunyai nilai negatif, berbentuk akar, atau bahkan berbentuk pecahan? Pelajari sifat-sifat lengkapnya di halaman ini agar semakin memahami bilangan eksponen.
Berbagai Jenis Bilangan Berpangkat
Berdasarkan tanda pangkat yang digunakan, ada empat jenis bilangan eksponen. Setiap jenisnya mempunyai formula dan sifat yang berbeda. Keempat jenis bilangan pangkat tersebut adalah bilangan pangkat dengan nilai positif, negatif, pangkat 0, dan bilangan pangkat pecahan.
1. Bilangan pangkat positif
Merupakan jenis bilangan pangkat yang bagian pangkatnya mempunyai angka atau nilai positif. Rumusnya adalah yang disebutkan sebelumnya, yaitu an=axaxaxax…xa. A merupakan bilangan pokok atau basis sedangkan n merupakan pangkatnya.
Dari rumus ini, bisa dijabarkan menjadi a yang kemudian dipangkatkan dengan n berarti a akan dikalikan dengan a hingga jumlahnya sama seperti pangkatnya. Agar lebih mudah dalam memahami jenis bilangan pangkat yang satu ini, coba perhatikan beberapa contohnya di bawah ini.
| Bilangan pangkat | Penjabaran | Hasil |
| 23 | 2x2x2 | 8 |
| 34 | 3x3x3x3 | 81 |
| 45 | 4x4x4x4x4 | 1.024 |
| 26 | 2x2x2x2x2x2 | 64 |
Dari beberapa contoh yang ada di atas, bisa disimpulkan bahwa jika suatu bilangan mempunyai pangkat yang lebih besar, nilai bilangan yang dihasilkan tentu saja akan menjadi lebih besar secara otomatis. Nilainya akan sangat besar jika basisnya atau bilangan pokoknya sendiri sudah besar.
2. Bilangan pangkat negatif
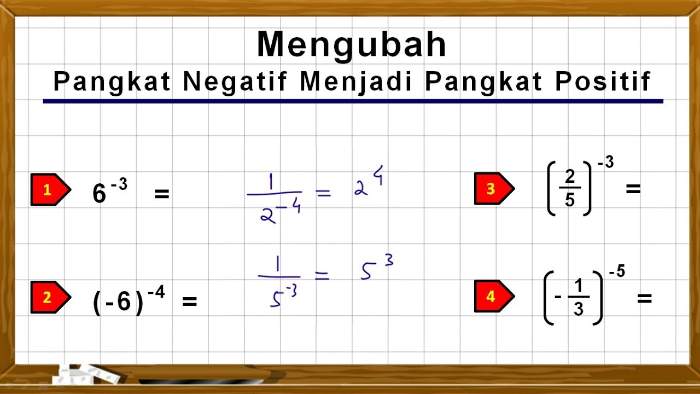
Setelah mengetahui jenis bilangan pangkat yang pertama, pelajari juga jenis bilangan pangkat yang berikutnya, yaitu bilangan pangkat negatif. Jenis bilangan pangkat yang satu ini merupakan kebalikan dari jenis yang sebelumnya. Jadi, pangkatnya merupakan bilangan negatif.
Rumus untuk bilangan berpangkat negatif adalah a-n=(1a)m. Rumus ini terlihat sedikit lebih rumit dibandingkan dengan rumus yang sebelumnya. A pada rumus ini masih sama dengan a pada jenis bilangan sebelumnya, yaitu berupa bilangan riil dan bukan merupakan angka 0.
Kemudian m merupakan bilangan bulat dengan nilai positif. Agar lebih mengerti seperti apa kira-kira penerapan bilangan pangkat negatif, pelajari contoh ini: 2-6=( 6 = = . Sifat bilangan pangkat ini tidak sama dengan sifat bilangan pangkat sebelumnya.
Pada bilangan pangkat negatif, jika pangkat negatifnya semakin besar, maka nilai bilangan yang dihasilkan justru akan menjadi semakin kecil.
3. Bilangan pangkat nol
Jenis yang berikutnya dari bilangan eksponen adalah bilangan dengan pangkat 0. Karena pangkatnya adalah 0, maka sebanyak apapun bilangan pokoknya, hasil yang akan diperoleh adalah 1. Rumus yang digunakan untuk bilangan pangkat 0 adalah a0=1.
Dalam rumus bilangan pangkat 0 ini, a merupakan bilangan riil tapi bukan berupa angka 0. Ada beberapa contoh yang bisa diperhatikan untuk lebih memahami bilangan pangkat 0. Beberapa contoh tersebut ada dalam tabel berikut ini.
| Bilangan pangkat | Hasil |
| 20 | 1 |
| 190 | 1 |
| 1.3450 | 1 |
| 456.5430 | 1 |
Sebenarnya bilangan pangkat 0 merupakan jenis bilangan pangkat yang paling mudah untuk dihafalkan dan dimengerti. Karena sebesar apapun bilangan pokok yang menjadi a tidak akan mempengaruhi hasilnya jika bertemu dengan pangkat 0. Hasilnya akan selalu 1.
4. Bilangan berpangkat pecahan
Dalam bilangan pangkat pecahan ini tersedia beberapa cara yang bisa digunakan untuk menyelesaikan soal yang ada. Tapi rumus yang paling umum dan paling sering digunakan untuk menyelesaikan bilangan pecahan adalah a1/m=p sehingga pm=a.
Rumus tersebut adalah untuk bilangan pangkat pecahan yang mempunyai nilai positif. Rumus lainnya adalah am/n=a(1/n)m. Dalam rumus bilangan pangkat pecahan ini, a merupakan bilangan riil dan bukan merupakan angka 0. Kemudian m menandakan bilangan bulat yang nilainya positif. Contohnya:
81/3=2 sehingga 23=8.
22/3=(21/3)2.
Berbagai Sifat Bilangan Eksponen
Saat akan mengoperasikan bilangan eksponen atau bilangan pangkat, jangan sembarangan melakukan perkalian. Pastikan untuk memahami dulu berbagai sifat yang terdapat di bilangan pangkat. Hal ini sangat penting karena berbagai sifat inilah yang menjadi acuan paling utama.
Berbagai sifat tersebut akan digunakan sebagai acuan utama saat akan mengoperasikan bilangan eksponen. Beberapa sifat tersebut adalah:
1. Penjumlahan pangkat
Jika ada perkalian antara dua atau beberapa angka berpangkat yang bilangan pokoknya atau basisnya sama, maka penjumlahan pangkat merupakan sifat yang akan diterapkan. Hal ini berarti sifat ini akan berlaku jika bilangan pangkat mempunyai basis yang sama.
Jika bilangan pangkat yang basisnya sama dikalikan, maka tinggal jumlahkan saja pangkatnya. Rumusnya adalah abxac=ab+c. Perlu diingat, sifat penjumlahan pangkat ini hanya bisa dilakukan jika kedua a mempunyai nilai yang sama. Misalnya sama-sama angka dua atau angka lainnya.
| Bilangan pangkat | Penjabaran | Hasil |
| 23x22 | 23+2=25 | 32 |
| 22x23x24 | 22+3+4=29 | 512 |
Dari dua contoh dalam tabel di atas, bilangan berpangkat dengan sifat penjumlahan pangkat berhasil dilakukan karena bilangan pokok atau basisnya sama, yaitu menggunakan angka dua. Kalau bilangan basisnya tidak sama, misalnya salah satunya 2 dan yang lainnya 3, sifat ini tidak berlaku,
2. Pengurangan pangkat
Sifat pengurangan pangkat ini mempunyai konsep dasar yang hampir sama dengan penjumlahan pangkat. Maksudnya, keduanya sama-sama bila dilakukan atau diterapkan jika bilangan pokok atau basisnya sama. Bedanya adalah sifat pengurangan pangkat berlaku jika basis yang sama akan dibagi.
Rumusnya adalah =ab-c, syaratnya adalah nilai b harus lebih besar dibandingkan dengan nilai c. Contohnya adalah =55-2=53. Sama dengan sifat penjumlahan pangkat, pengurangan pangkat juga tidak bisa berlaku kalau a-nya atau bilangan pokoknya tidak mempunyai nilai yang sama.
3. Perkalian pangkat
Sifat lain dalam bilangan berpangkat adalah perkalian pangkat yang bisa digunakan jika bilangan pangkat akan dipangkatkan lagi. Hal ini berarti adanya suatu bilangan yang sudah dipangkat kemudian dipangkatkan lagi. Maka pangkat tersebut perlu dikalikan. Rumusnya adalah (ab)c=abxc.
| Bilangan pangkat | Penjabaran | Hasil |
| (52)3 | 52×3 | 56 |
| (23)2 | 23×2 | 26 |
Sifat ketiga bilangan pangkat ini juga sama dengan dua sifat yang sebelumnya, yaitu hanya berlaku untuk suatu bilangan pangkat yang dikalikan dengan bilangan pangkat dengan nilai yang sama. Jadi jika a-nya atau bilangan pokoknya berbeda, maka pangkatnya tidak bisa dikalikan.
4. Pembagian pangkat
Sifat lainnya yang dimiliki oleh bilangan eksponen atau bilangan pangkat adalah pembagian pangkat. Sifat yang satu ini berlaku pada bilangan akar. Sebelum mempelajari pembagian pangkat, sangat penting untuk mempelajari perubahan bentuk pada bilangan akar terlebih dahulu.
Ketika suatu bilangan di akar, bilangan tersebut akan diubah dalam bilangan pangkat pecahan. Rumus yang digunakan adalah b=ab/2. Jika sudah memahami konsep yang satu ini, pembagian pangkat akan menjadi lebih mudah untuk dipahami.
Sifat yang satu ini bisa digunakan untuk bilangan pangkat tertentu yang diakar. Perlu diingat yang akan dibagi adalah bagian pangkatnya dan bukan bilangan pokoknya. Agar lebih mudah memahaminya, perhatikan contoh dari sifat-sifat bilangan pangkat yang satu ini.
| Bilangan pangkat | Penjabaran |
| b=ab/2 | 5=55/2 |
| 5=a5/3 | b=55/3 |
5. Sifat bilangan berpangkat satu
Dalam dunia matematika, angka 1 adalah suatu angka yang sangat ikonik. Alasannya adalah pembagian maupun perkalian apapun yang melibatkan angka satu biasanya menghasilkan bilangan yang dikalikan atau dibagikan. Hal yang sama berlaku juga dalam dunia perpangkatan.
Pangkat sendiri sebenarnya merupakan bentuk yang lebih sederhana dari perkalian bilangan pokok yang kemudian dipangkatkan. Artinya, angka 23 berarti angka 2 akan dikalikan sebanyak 3 kali sehingga menghasilkan angka 8. Jadi angka 21 berarti angka 2 tidak perlu dikalikan dengan apapun.
Sehingga bisa disimpulkan bahwa apapun bilangan yang digunakan sebagai basis atau bilangan pokok, kalau pangkatnya adalah angka 1 maka hasilnya sudah pasti adalah bilangan pokok itu sendiri. Rumus yang digunakan adalah a1=a.
| Bilangan pangkat | Hasil |
| 21 | 2 |
| 351 | 35 |
| 7651 | 765 |
| 977.5461 | 977.546 |
| 2.647.3561 | 2.647.356 |
6. Sifat bilangan pangkat negatif
Bilangan pangkat harus memenuhi beberapa persyaratan. Salah satu syaratnya adalah menjadi suatu bagian dari bilangan riil. Berbagai penjelasan sebelumnya membahas bilangan pangkat dengan nilai positif. Tapi jangan melupakan bilangan pangkat dengan sifat negatif.
Dalam bilangan pangkat dengan sifat negatif, rumus yang digunakan adalah a-1=1/ab. Dari rumus ini, bisa disimpulkan kalau pangkat negatif nantinya bisa membentuk sebuah pecahan. Dalam rumus ini, pembilang yang digunakan adalah angka 1 sedangkan penyebutnya merupakan bilangan pokok.
Berbagai Kegunaan Bilangan Eksponen dalam Kehidupan
Beberapa orang mungkin bertanya-tanya apa saja gunanya mempelajari bilangan pangkat. Bilangan pangkat mengandung berbagai rumus yang sangat bermanfaat bagi kehidupan setiap hari. Konsep pangkat bisa digunakan dalam berbagai aspek kehidupan. Contohnya adalah:
- Untuk memprediksi hasil ternak, caranya adalah dengan memanfaatkan bilangan geometri atau konsep rasio.
- Konsep dagang dengan perhitungan untung dan rugi, patokan yang digunakan adalah harga barang dan kuantitas.
- Dunia kimia menggunakan konsep bilangan pangkat saat akan mencari pH yang terdapat dalam setiap jenis larutan.
- Ilmu fisika juga membutuhkan konsep bilangan pangkat, konsep ini akan digunakan dalam mencari induksi magnetik setiap kumparan magnet.
Masih banyak manfaat lain yang bisa diperoleh dengan menggunakan atau memanfaatkan konsep pangkat dalam aspek kehidupan lainnya. Pastikan untuk mempelajari bilangan pangkat dengan serius, serta mengerti seluruh sifat yang ada dalam bilangan pangkat.
Bilangan berpangkat merupakan salah satu bilangan yang sangat dibutuhkan dalam ilmu matematika. Berkat bilangan pangkat, perhitungan yang rumit bisa disederhanakan. Persamaan juga menjadi lebih mudah diselesaikan berkat adanya berbagai rumus bilangan pangkat ini.